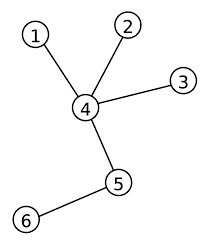
Prove that every tree has at most one perfect matching.

Since every tree with 2 or more vertices is 2-chromatic. We see that a tree with even no. of vertices will have perfect matching as all vertices with the same color can be grouped together and a matching can be established between the two groups. If the tree has odd number of vertices,then no perfect matching can be established for obvious reason.    [proved
]

Comments

Post a Comment

Popular posts from this blog

Show that number of pendant vertices in a binary tree is (n+1)/2 ,where n is the number of vertices in the tree.

Image
The number of vertices of odd degree in an undirected graph is even,(N-1) is even.  Therefore, n is odd. Let p be the number of pendant vertices. 2+p+3(n- p-1) = 2(n-1) or, 3n-2n-3+4 = 2p or, 2p = n+1 or, P = (n+1)/2 Hence, the number of pendant vertices is (n+1)/2. Also, see : 1.)  Graph Theory and Tree 2.)  The Reflection about line yx is.......... 3.)  Prove that a simple graph with n vertices and k components can have at most 1/2(n-k)(n-k-1) edges. 4.)  Show for what condition rotation and scaling are commutative. 5.) Vector in R space 6.) Prove that every tree has at most one perfect matching. 7.)  Prove that every tree with 2 or more vertices is 2-chromatic. 8.)  Show that every Bi-partite graph is 2 chromatic. 9.) Prove that the number of circular permutations of n different objects is (n-1)! . 10.)  State the "Pigeon Hole Principle" and the " Generalised pigeon Hole principle".
Read more

Prove that every tree with 2 or more vertices is 2-chromatic.

Image
Since a tree is connected and has no cycle if one starts coloring any one vertex with a specific color and keeps on coloring every alternate vertex with another color, the entire graph can be colored with only two colors and since there is one and only one path between any two vertices in a tree, no two vertices will have the same color. Hence every Tree with 2 or more vertices is 2-Chromatic.    [Proved]                                                                 FIG (I)                                                                  FIG (II)
Read more

Top 5 websites to learn coding Online

Image
Now, A Days Technology became our Daily Life partner. Sometimes we people are wondering how this page, website, Blog ,Game works .Then,Our Mind  starts searching for Real phenomenon .How this site works ,why this website is different from others,How the widget is different from others ,How e-commerce website works. So, The answer of all of the above is "CODING". Being a programmer ,i think without Coding Digital Word is Nothing. So, you need to learn Coding if you are interested in Digital world. Myths about coding is that It is Hard to Understand & Hard to Write.There is nothing like this.Just you have to do some basic Homework daily and continuation in learning.Learn Coding like a Interesting Puzzle and solve like a "SUDUKO" Game. Let's Start: Kids Section: For kids Go for  Tynker   (Android/IOS) and  Hopscotch   (IPAD) .These sites are the best tutor of kids ,they teach coding in the form of Games & Puzzles.
Read more