Show that number of pendant vertices in a binary tree is (n+1)/2 ,where n is the number of vertices in the tree.
The number of vertices of odd degree in an undirected graph is even,(N-1) is even.
Therefore, n is odd.
Let p be the number of pendant vertices.
2+p+3(n- p-1) = 2(n-1)
or, 3n-2n-3+4 = 2p
or, 2p = n+1
or, P = (n+1)/2
Hence, the number of pendant vertices is (n+1)/2.
Also, see :
1.) Graph Theory and Tree
2.) The Reflection about line yx is..........
3.) Prove that a simple graph with n vertices and k components can have at most 1/2(n-k)(n-k-1) edges.
4.) Show for what condition rotation and scaling are commutative.
5.)Vector in R space
6.)Prove that every tree has at most one perfect matching.
7.) Prove that every tree with 2 or more vertices is 2-chromatic.
8.) Show that every Bi-partite graph is 2 chromatic.
9.)Prove that the number of circular permutations of n different objects is (n-1)! .
10.) State the "Pigeon Hole Principle" and the " Generalised pigeon Hole principle".
2.) The Reflection about line yx is..........
3.) Prove that a simple graph with n vertices and k components can have at most 1/2(n-k)(n-k-1) edges.
4.) Show for what condition rotation and scaling are commutative.
5.)Vector in R space
6.)Prove that every tree has at most one perfect matching.
7.) Prove that every tree with 2 or more vertices is 2-chromatic.
8.) Show that every Bi-partite graph is 2 chromatic.
9.)Prove that the number of circular permutations of n different objects is (n-1)! .
10.) State the "Pigeon Hole Principle" and the " Generalised pigeon Hole principle".
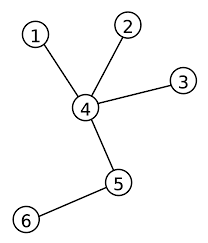



Comments