Graph theory and tree.
Introduction :
Graph theory may be said to have its beginning in 1736 when Euler considered the (general case of the) Konigsberg bridge problem. Does there exist a walk crossing each of the seven bridges of Konigsberg exactly once?
It took 200 years before the first book on graph theory was written. This was "Theorie der endlichen und unendlichen Graphen" by koing in 1936.Since,then graph theory has developed into an extensive and popular branch of mathematics,which has been applied to many problems in mathematics, computer science and other scientific and not-s-scientific areas.
There are no standard notations for graph theoretical objects. This is natural because the names one uses for the objects reflect the applications. Thus, for instance, if we consider a communication network (say, for email) as a graph, the computers taking part in this network, are called nodes rather than vertices or points.On the other hand, other names are used for molecular structures in chemistry, flow charts in programming human relations in social sciences, and so on.
Indeed graph theory has the advantage that it contains easily formulated open problems that can be started early in history. Finding a solution to any of these problems is another matter.
Notations & Notions :
- For a finite set X,| X | denotes its size (cardinality, the number of its elements).
- Let [1,n]={1,2,3................n},and in general [i,n]={i,i+1,i+2.........n} for integers i ≤ n.
- For a real number x, the floor and the ceiling of x are the integers ⎡x⎤=max{k ∈ 𝐙 | k ≤ x} and ⎡x⎤=min {k ∈ 𝐙 | x ≤ k}
- A family {X1, X2.............Xk} of subsets X¡ ⊆ X of a set X is a partition of X if X= ∪X¡ and X¡ ∩ Xj =∅ for all different i and j.
- For two sets X and Y, X×Y={(x,y)⎪ x ∈ X,y ∈ Y} is their cartesian product and, X∆Y=(X\Y)∪(Y\X) is their symmetric difference. Here X\Y={x⎪x ∈ X,x ∉ Y}.
- Two integers n,k ∈ N (often n=⎪X⎪ and k=⎪Y⎪ for sets X and Y) have the same parity if both are even, or both are odd, that is, if n ≡ k(mod2).Otherwise, they have opposite parity.
Graph theory has abundant examples of NP-complete problems.Intuitively, a problem is in P if there is an efficient (practical) algorithm to find a solution to it.On the other hand,a problem is in NP,if it is first efficient to guess a solution and then efficient to check that this solution is correct.It is conjectured (and not known) that P ≄NP. This is one of the great problems in modern mathematics and theoretical computer science . If the guessing in NP-problems can be replaced by an efficient systematic search for a solution, then P=NP. For anyone, NP-complete problem, if it is in P, then necessarily P=NP.
Graph and their plane figures :
Let V be a finite set and denote by E(V)={{u,v}⎪ u,v ∈ V,u ≠ v} the 2-sets of V.i.e., subsets of two distinct elements.
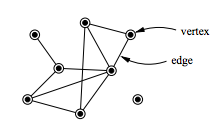
Definition 1: A pair G=(V, E) with E ⊆ E(V) is called a graph (on V).The elements of V are the vertices of G and those of E the edges of G.The vertex set of a graph G is denoted by Vg and its edge by Eg. Therefore G=(Vg, Eg).
In literature, graphs are also called simple graphs; vertices are called nodes or points; edges are called lines or links. The list of alternatives is long(but still finite).A pair {u,v} is usually written simply as uv. Notice that then uv=vu.In order to simplify notations,we also write v ∈ G and e ∈ G instead of v∈Vg and e ∈ Eg.
Definition 2: For a graph G, we denote vg =⎪Vg⎪ and eg= ⎪Eg⎪. The number vg of the vertices is called the order of G and eg is the size of G.For an edge e = uv ∈ G,the vertices u and v are its ends. vertices u and v are adjacent or neighbours, if uv ∈ G.Two edges e1=uv and e2=uw having a common end,are adjacent with each other.
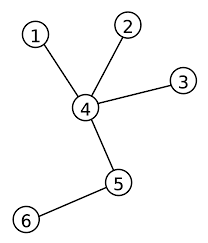
A graph G can be represented as a plane figure by drawing a line (or a curve) between the points u and v (representing vertices ) if e=uv is an edge of G.The figure below is a geometric representation of the graph G with Vg={v1,v2,v3,v4,v5,v6} and Eg={v1v2,v1v3,v2v3,v2,v4,v5v6}.
Often we shall omit the identities (names v) of the vertices in our figures, in which case the vertices are drawn as anonymous circles.
Graphs can be generalized by allowing loops vv and parallel(or multiple) edges between vertices to obtain a multigraph G=(V, E, ψ) , where E=(e1,e2,e3..............em) is a set (of symbols ) and
ψ :E ￫ E(V) ∪ {vv⎪v ∈ V} is a function that attaches an unordered pair of vertices to each e ∈ E: ψ(e) =uv.
Note that,we can have ψ(e1)=ψ(e2).This is drawn in the figure of G by placing two (parallel) edges that connect the common ends.There is also a multigraph G with vertices V={a,b,c} and edges ψ(e1)=aa ,ψ(e2)=ab ,ψ(e3)=bc and ψ(e4)=bc.
Definition 3: We also study directed graphs or digraphs D=(V,E), where the edges have a direction, that is, the edges are ordered: E ⊆ V×V .In this case UV ≠ vu.
Comments