Isomorphism of graph.
Definition:
Two graphs G and H are isomorphic, denoted by G ≅ H, if there exists a bijection α:Vg➝Vh such that :
uv ∈ Eg ⇔ α(u)α(v) ∈ Eh ; for all u,v ∈ G
Hence G and H are isomorphic if the vertices of H are remaining of those of G.Two isomorphic graphs enjoy the same graph-theoretical properties and they are often identified.In particular,all isomorphic graphs have the same plane figures (excepting the identities of the vertices). This shows in the figures, where we tend to replace the vertices by small circles and talk of 'the graph' although there are, in fact, infinitely many such graphs.Example 1: The following graphs are isomorphic . Indeed, the required isomorphism is given by
Isomorphism Problem: Does there exist an efficient algorithm to check whether any two given graphs are isomorphic or not?
The following table lists the number a^{n/2} of all graphs on a given set of n vertices and the number of all non-isomorphic graphs on n vertices. It tells that at least for computational purposes an efficient algorithm for checking whether two graphs are isomorphic or not would be greatly appreciated.
n
|
1
|
2
|
3
|
5
|
6
|
7
|
8
|
9
|
graphs
|
1
|
2
|
8
|
1024
|
32768
|
2097152
|
268435456
|
2^36
|
Non-isomorphic
|
1
|
2
|
4
|
34
|
156
|
1044
|
12346
|
274668
|
Other Representations:
Plane figures catch graphs for our eyes, but if a problem on graphs is to be programmed, then these figures are, to say the least, unsuitable. Integer matrices are ideal for computers since every respectable programming language has array structures for these and computers are good in crunching numbers.
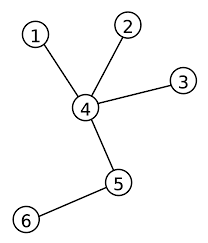
Let Vg={v1,v2...............vn} be ordered .The adjacency matrix of G is the n x n matrix M with entries Mij=1 or Mij=0 according to whether vivj ∈ G or vivj ∉ G.For instance, the graphs in Example 1.1 have an adjacency matrix on the right . Notice that the adjacency matrix is always symmetric (with respect to its diagonal consisting of zeros.)
A graph has usually many different adjacency matrices, one for each ordering of its set Vg of vertices. The following result is obvious from the definitions.
Theorem 1: Two graphs G and H are isomorphic iff they have a common adjacency matrix. Moreover , two isomorphic graphs have exactly the same set of adjacency matrices.
Graphs can also be represented by sets .For this,let X={X1,X2,................Xn} be a family of subsets of a set X and define the intersection graphs Gx as the graph with vertices X1,X2......Xn and edges XiXj for all i and j (i≠j) with Xi ⋂ Xj ≠ Φ.
Theorem 2: Every graph is an intersection graph of some family of subsets................................
Proof: Let G be a graph and define, for all v ∈ G, a set .................................................................
Xv ={{v,u}丨vu ∈ G}.
Then, Xu ⋂ Xv ≠ Φ if and only if uv ∈ G.
Let s(G) be the smallest size of a base set X such that G can be represented as an intersection graph of a family of subsets of X, that is,
s(G)=min{| X |│G ≅ Gx for some X ⊆ 2^X}.
How small can s(G) be compared to the order vG(or the size εG) of the graph? It was shown by KOU, STOCKMEYER and WONG (1976) that it is algorithmically difficult to determine the number s(G) -the problem is NP-complete.
Example 2: As yet another example, let A ⊆ N be a finite set of natural numbers, and let G(A)=(A, E) be the graph with rs ∈ E iff r and s (for r ≠ s)have a common divisor >1. As an exercise, we state: All graphs can be represented in the form G(A) for some set A of natural numbers.
THANK YOU






Comments